Transport-Phenomena Assignment 1st Release

Velocity profiles and the stress components. For each of the following velocity distributions, draw a meaningful sketch showing the flow pattern. Then find all the components for the Newtonian fluid. The parameter b is a constant.

Below is the Python codes solution:

    
# Todo: Problem 1 (a)
import numpy as np
import matplotlib.pyplot as plt

b = 1
x = np.linspace(-3, 3, 20)
y = np.linspace(-3, 3, 20)
X, Y = np.meshgrid(x, y)
vx = b * Y
vy = np.zeros_like(X)  # vy = 0
gradient_magnitude = np.sqrt(vx**2 + vy**2)

plt.figure(figsize=(8, 6))
quiver_plot = plt.quiver(
    X, Y, vx, vy, gradient_magnitude, cmap='viridis', scale=10, pivot='middle',
    headwidth=8, headlength=6
)
plt.colorbar(quiver_plot, label='Gradient Magnitude')
plt.title('Velocity Field ($v_x = by$, $v_y = 0$) | Range: [-3, 3]', fontsize=14, color='midnightblue')
plt.xlabel('x', fontsize=12, color='darkblue')
plt.ylabel('y', fontsize=12, color='darkblue')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.5)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5, alpha=0.7)
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.show()

Output:

Here’s a visualization under condition (b):

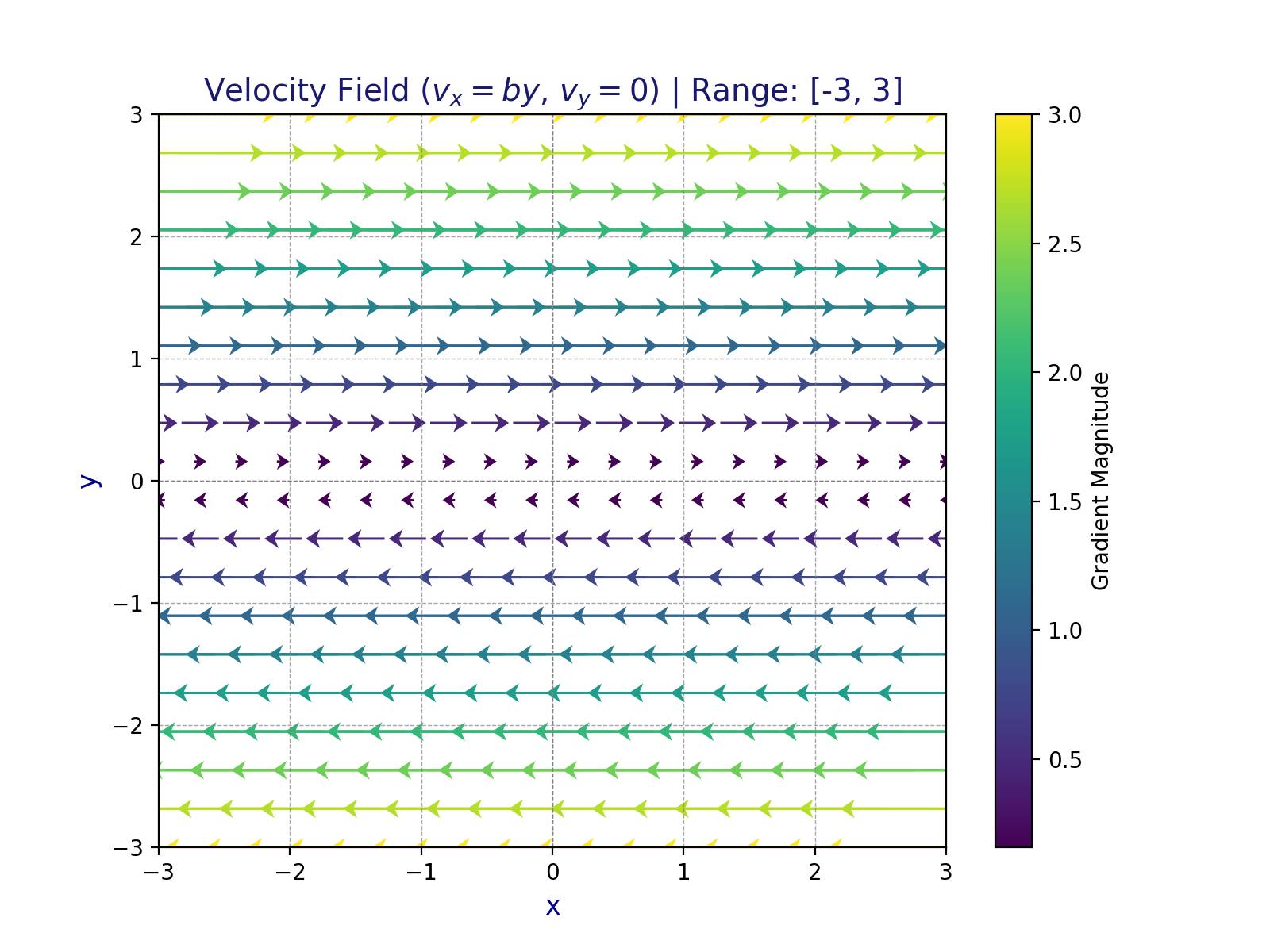
Factorial Calculation Example 
    
# TODO: Problem 1 (b)
b = 1
x = np.linspace(-3, 3, 20)
y = np.linspace(-3, 3, 20)
X, Y = np.meshgrid(x, y)
vx = b * Y
vy = b * X
gradient_magnitude = np.sqrt(vx**2 + vy**2)

plt.figure(figsize=(8, 6), dpi=200)
quiver_plot = plt.quiver(
    X, Y, vx, vy, gradient_magnitude, cmap='viridis', scale=10, pivot='middle', headwidth=8, headlength=6
)
plt.colorbar(quiver_plot, label='Gradient Magnitude')
plt.title('Velocity Field: $v_x = by$, $v_y = bx$ | Range: [-3, 3]', fontsize=14, color='midnightblue')
plt.xlabel('x', fontsize=12, color='darkblue')
plt.ylabel('y', fontsize=12, color='darkblue')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.5)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5, alpha=0.7)
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.show()

Output:

Here’s a visualization under condition (b):

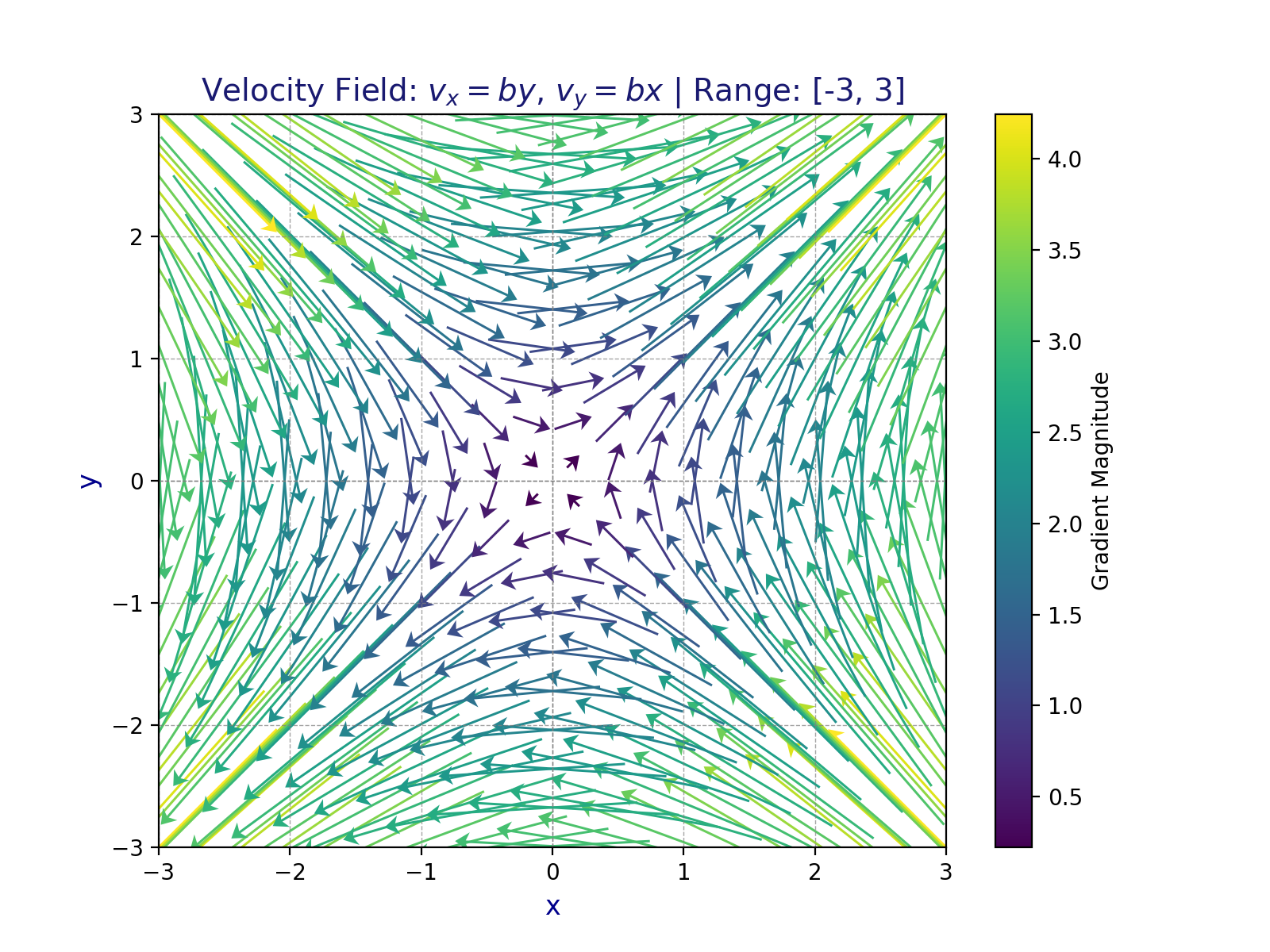
Factorial Calculation Example 
    
# TODO: Problem 1 (c)
# Todo: Problem 1 (c)
b = 1
x = np.linspace(-3, 3, 20)
y = np.linspace(-3, 3, 20)
X, Y = np.meshgrid(x, y)
vx = -b * Y
vy = b * X
gradient_magnitude = np.sqrt(vx**2 + vy**2)

plt.figure(figsize=(8, 6), dpi=200)
quiver_plot = plt.quiver(
    X, Y, vx, vy, gradient_magnitude, cmap='viridis', scale=10, pivot='middle', headwidth=8, headlength=6
)
plt.colorbar(quiver_plot, label='Gradient Magnitude')
plt.title('Velocity Field: $v_x = -by$, $v_y = bx$ | Range: [-1.5, 1.5]', fontsize=14, color='midnightblue')
plt.xlabel('x', fontsize=12, color='darkblue')
plt.ylabel('y', fontsize=12, color='darkblue')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.5)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5, alpha=0.7)
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.show()

Output:

Here’s a visualization under condition (c):

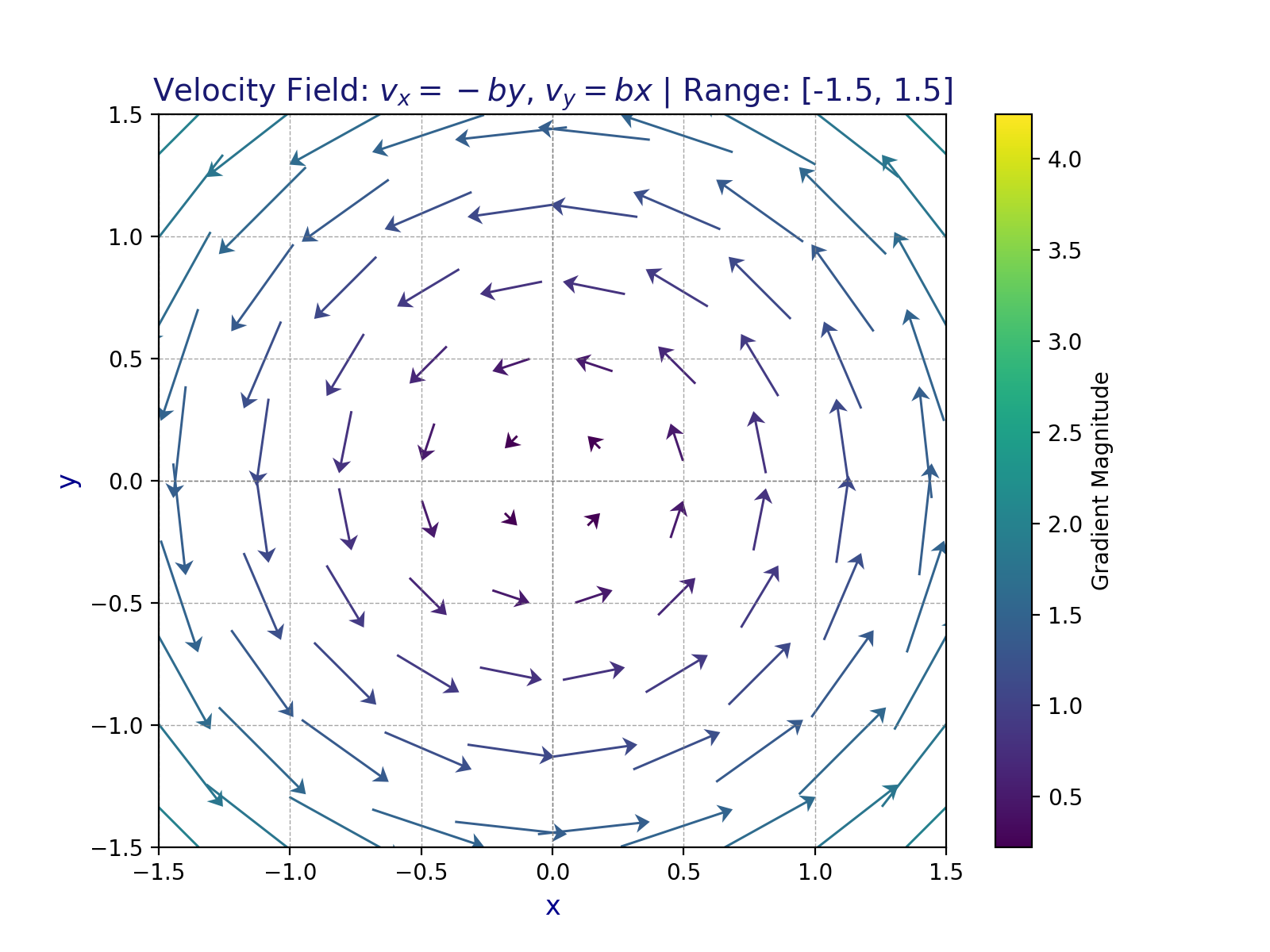
Factorial Calculation Example 
    
# Todo: Problem 1 (d)
b = 1
x = np.linspace(-1, 1, 8)
y = np.linspace(-1, 1, 8)
z = np.linspace(-1, 1, 8)
X, Y, Z = np.meshgrid(x, y, z)
vx = -0.5 * b * X
vy = -0.5 * b * Y
vz = b * Z
velocity_magnitude = np.sqrt(vx**2 + vy**2 + vz**2)
fig = plt.figure(figsize=(12, 9), dpi=200)
ax = fig.add_subplot(111, projection='3d')
norm = plt.Normalize(vmin=velocity_magnitude.min(), vmax=velocity_magnitude.max())
cmap = plt.get_cmap('viridis')
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
color = sm.to_rgba(velocity_magnitude.flatten())
quiver_plot = ax.quiver(X, Y, Z, vx, vy, vz, length=0.15, normalize=True, color=color, alpha=0.8, linewidth=2)
cbar = fig.colorbar(sm, ax=ax, label='Velocity Magnitude')
ax.set_title('3D Velocity Field: $v_x = -0.5bx$, $v_y = -0.5by$, $v_z = bz$ | Range: [-1, 1]', fontsize=14, color='midnightblue')
ax.set_xlabel('x', fontsize=12, color='darkblue')
ax.set_ylabel('y', fontsize=12, color='darkblue')
ax.set_zlabel('z', fontsize=12, color='darkblue')
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])
ax.view_init(elev=30, azim=45)
plt.show()

Output:

Here’s a visualization under condition (d):

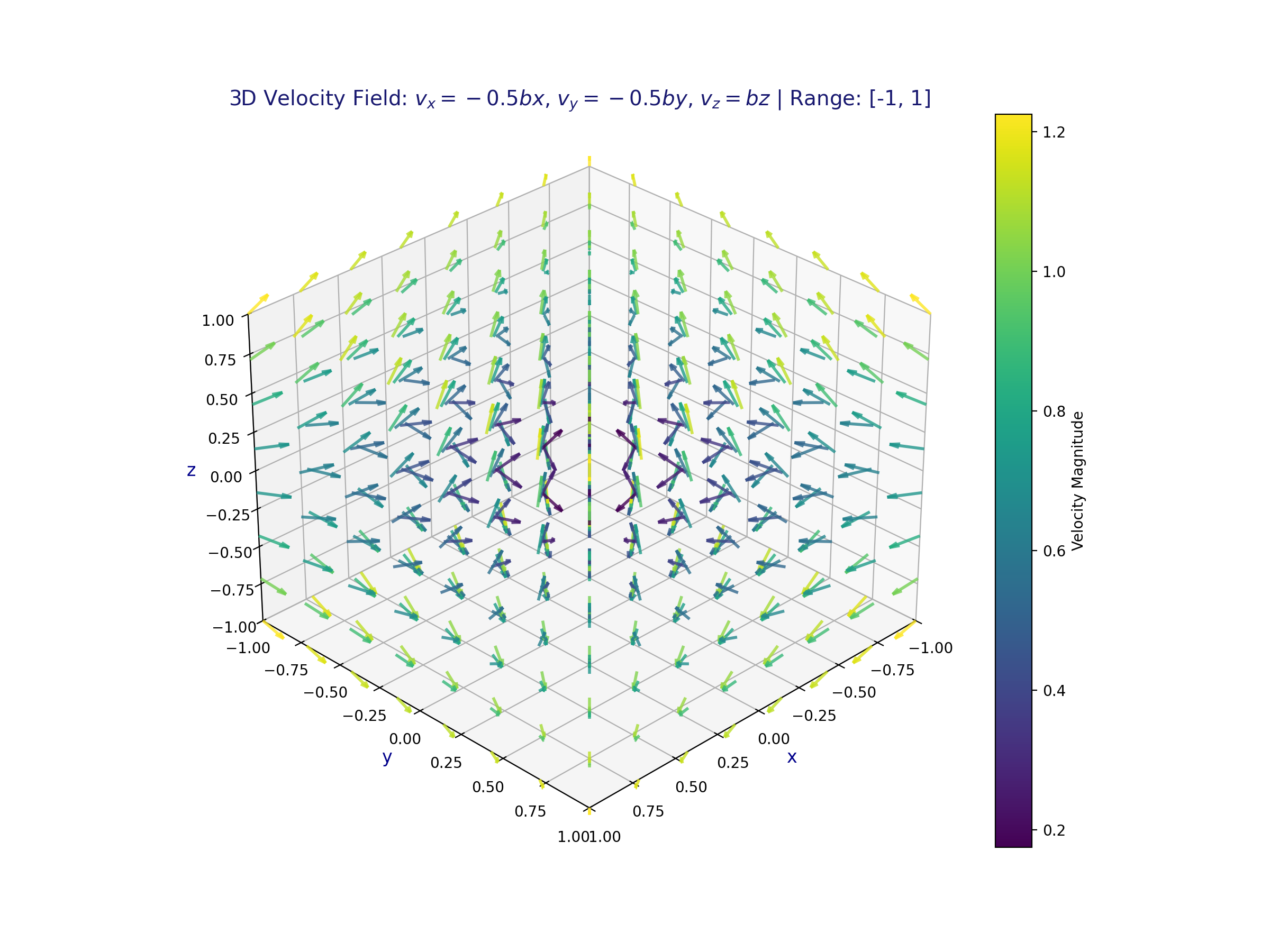
Factorial Calculation Example